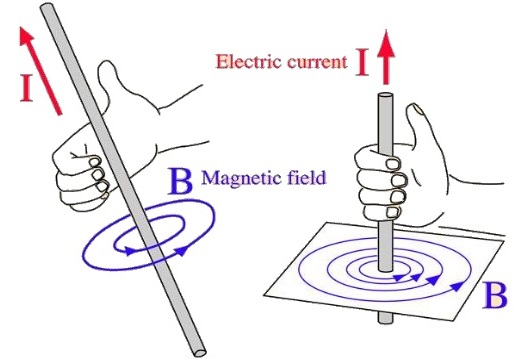
What is Biot-Savart Law?
Biot and Savart conducted many experiments on the force exerted by an electric current on a nearby magnet and at last they derived a mathematical expression that gives the magnetic field at some point in space due to a current passing through a conductor.
biot savart law statement
The biot savart law states that:
Magnetic field (B) along vertical current carrying conductor/wire in a closed surface is directly proportional to the current(I) and inversely proportional to the perpendicular distance from the point of conductor/wire.
biot savart law derivation
Now let us understand in further details:
Consider a current carrying conductor in a closed surface.
Mathematically,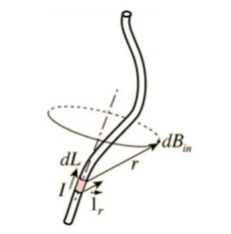
B∝ I/r
B=KI/r
Where K= propotionality constant and its value depends on nature of closed surface where conducter is situated
K= µ 0 /2 π
µ 0= permiability of free space = 4π x 10e-7 h/m
K= 2 x 10e-7 h/m
B= µ 0 I/2πr
Magnetostatics
If charges are moving with constant velocity, a static magnetic (or magnetostatic) field is produced. Thus, magnetostatic fields originate from currents (for instance,direct currents in current-carrying wires). Most of the equations we have derived for the electric fields may be readily used to obtain corresponding equations for magnetic fields if the equivalent analogous quantities are substituted
The magnetic field intensity dH produced at a point P by the differential current element Idl is proportional to the product of Idl and the sine of the angle α between the element and the line joining P to the element and is inversely proportional to Idl sin α the square of the distance R between P and the element. 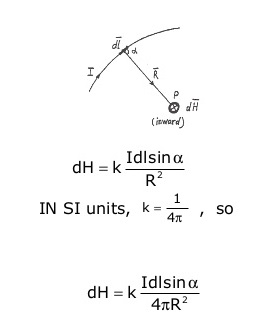
Difference Between Biot-Savart law and Ampere’s law
Biot-Savart law and Ampere’s law both help in finding magnetic field distributions, but Ampere’s law takes symmetry into account as its a closed line integral (Amperian loop). Both laws can be used to calculate the net magnetic field produced at a point by various distributions of current. Situations where Ampere’s law can be used include Magnetic field of a solenoid and Magnetic field of a toroid.
Magnetic Flux Density
The magnetic flux density vector is related to the magnetic field intensity H by the following equation
B = µ H, T (tesla) or Wb/m2
Where µ is the permeability of the medium. Except for ferromagnetic materials ( such as cobalt, nickel, and iron), most materials have values of µ very nearly equal to that for vacuum,

The magnetic flux through a given surface S is given by

Law of conservation of magnetic flux or Gauss’s law for magnetostatic field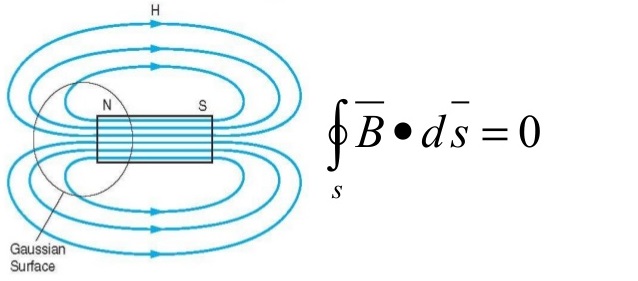
∇•B = 0∇ × B = µ0 J —-> ∇• J = 0
There are no magnetic flow sources, and the magnetic flux lines always close upon themselves. There are three ways in which force due to magnetic fields can be experienced
- Due to moving charge particle in a B field
- On a current element in an external field
- Between two current elements
Discover more from Electrical Engineering 123
Subscribe to get the latest posts sent to your email.