Because of its widespread use, we will concentrate on addition and subtraction for Two’s Complement representation.
The nice feature with Two’s Complement is that addition and subtraction of Two’s complement numbers works without having to separate the sign bits (the sign of the operands and results is effectively built-into the addition/subtraction calculation).
Remember: −2n−1 ≤ Two’s Complement ≤ 2n−1 − 1
−8 ≤ x[4] ≤ +7
−128 ≤ x[8] ≤ +127
−32768 ≤ x[16] ≤ +32767
−2147483648 ≤ x[32] ≤ +2147483647
What if the result overflows the representation?
If the result of an arithmetic operation is to too large (positive or negative) to fit into the resultant bit-group, then arithmetic overflow occurs. It is normally left to the programmer to decide how to deal with this situation.
Two’s Complement Addition Method
Add the values and discard any carry-out bit.
Examples: using 8-bit two’s complement numbers.
- Add −8 to +3
(+3) 0000 0011 +(−8) 1111 1000 ----------------- (−5) 1111 1011
- Add −5 to −2
(−2) 1111 1110 +(−5) 1111 1011 ----------------- (−7) 1 1111 1001 : discard carry-out
Overflow Rule for Addition
If 2 Two’s Complement numbers are added, and they both have the same sign (both positive or both negative), then overflow occurs if and only if the result has the opposite sign.
Overflow never occurs when adding operands with different signs. i.e.
- Adding two positive numbers must give a positive result
- Adding two negative numbers must give a negative result
Overflow occurs if:
(+A) + (+B) = −C
(−A) + (−B) = +C
Example: Using 4-bit Two’s Complement numbers (−8 ≤ x ≤ +7)
(−7) 1001 +(−6) 1010 ------------ (−13) 1 0011 = 3 : Overflow (largest −ve number is −8) A couple of definitions:
| Subtrahend: | what is being subtracted |
| Minuhend: | what it is being subtracted from |
Example: 612 - 485 = 127
485 is the subtrahend, 612 is the minuhend, 127 is the result
Two’s Complement Subtraction
Normally accomplished by negating the subtrahend and adding it to the minuhend. Any carry-out is discarded.
Example: Using 8-bit Two’s Complement Numbers (−128 ≤ x ≤ +127)
(+8) 0000 1000 0000 1000 −(+5) 0000 0101 -> Negate -> +1111 1011 —– ———– (+3) 1 0000 0011 : discard carry-out
Overflow Rule for Subtraction
If 2 Two’s Complement numbers are subtracted, and their signs are different, then overflow occurs if and only if the result has the same sign as the subtrahend.
Overflow occurs if
- (+A) − (−B) = −C
- (−A) − (+B) = +C
Example: Using 4-bit Two’s Complement numbers (−8 ≤ x ≤ +7)
Subtract −6 from +7
(+7) 0111 0111
−(−6) 1010 -> Negate -> +0110
---------- -----
13 1101 = −8 + 5 = −3 : Overflow
Number Circle for 4-bit Two’s Complement Numbers
Numbers can be added or subtracted by moving round the number circle
- Clockwise for addition
- Anti-Clockwise for subtraction (addition of a negative number)
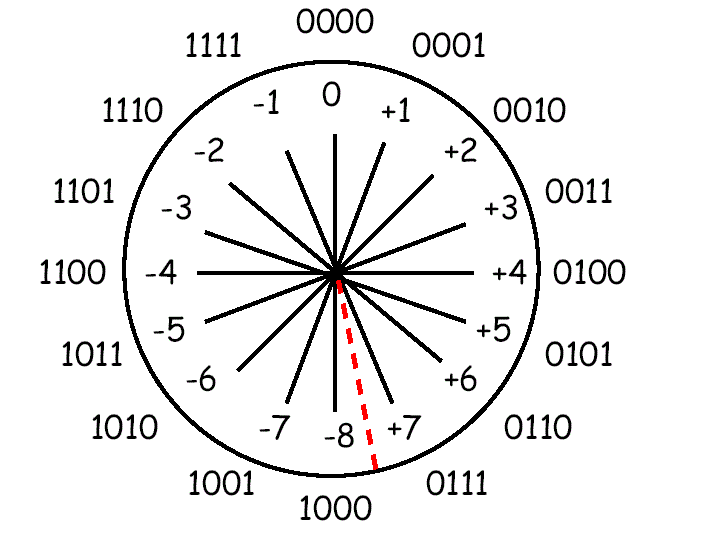
Overflow occurs when a transition is made
- from +2n−1−1 to −2n−1 when adding
- from −2n−1 to +2n−1−1 when subtracting
Summary About Two’s Complement
Addition
- Add the values, discarding any carry-out bit
Subtraction
- Negate the subtrahend and add, discarding any carry-out bit
Overflow
- Occurs when adding two positive numbers produces a negative result, or when adding two negative numbers produces a positive result. Adding operands of unlike signs never produces an overflow
- Notice that discarding the carry out of the most significant bit during Two’s Complement addition is a normal occurrence, and does not by itself indicate overflow
- As an example of overflow, consider adding (80 + 80 = 160)10, which produces a result of −9610 in 8-bit two’s complement:
01010000 = 80 + 01010000 = 80 -------------- 10100000 = −96 (not 160 because the sign bit is 1.) (largest +ve number in 8 bits is 127)
Multiplication and Division
No problem with unsigned (always positive) numbers, just use the same standard techiques as in base 10 (remembering that x[n] × y[n] = z[2n])
- Multiplication Example 11001012 × 1111012 (10110 × 6110)
1100101 10110 × 111101 × 6110 ------- 1100101 +1100101 +1100101 +1100101 +1100101 ------------- ????????????? -------------Easier to use intermediary results:
1100101 10110 × 111101 × 6110 ------- 1100101 +1100101 ---------- 111111001 +1100101 ------------ 10100100001 +1100101 ------------- 101101110001 +1100101 ------------- 1100000010001 = 409610 + 204810 + 1610 + 1 = 616110 ------------- - Division Example: 1001012 ÷ 1012 (3710 ÷ 510)
111 result = 710 ------- 101)100101 −101 --- 1000 −101 --- 111 −101 --- 10 remainder = 210 ---
Multiplication in Two’s complement cannot be accomplished with the standard technique since, as far as the machine itself is concerned, for Y[n]:
−Y º 0 − Y º 2n − Y
since, when subtracting from zero, need to “borrow” from next column leftwards.
Example:
| −1910 in 8-bits | = (28 − 19)10 |
| = 25610 − 1910 | |
| = 23710 | |
| = 111011012 unsigned | |
| = −27 + 26 + 25 + 23 + 22 + 20 | |
| = −128 + 64 + 32 + 8 + 4 + 1 | |
| = −128 + 109 | |
| = −1910 in Two’s Complement |
Consider X × (−Y)
Internal manipulation of −Y is as 2n − Y
Therefore X × (−Y) = X × (2n − Y) = 2n × X − X × Y
However the expected result should be 22n − (X × Y)
since x[n] × y[n] = z[2n]
Can perform multiplication by converting the Two’s Complement numbers to their absolute values and then negating the result if the signs of the operands are different. Similar for Two’s Complement division. Can convert the operands to their absolute values, perform the division, and then negating the result if the signs of the operands are different. Most contemporary architectures implement more sophisticated algorithms for multiplication and division of Two’s Complement numbers.
Refer below link for full course about Computer Architecture.
http://www.doc.ic.ac.uk/~eedwards/compsys/index.html
Discover more from Electrical Engineering 123
Subscribe to get the latest posts sent to your email.

