Numbering System and Digital Logic [Simplified]

There are different numbering systems used in digital electronic circuits and computers. However, the numbering system used in one type of circuit may be different to that of another type of circuit, for example, the memory of a computer would use hexadecimal numbers while the keyboard uses decimal numbers.

The different number systems are

Decimal – The decimal numbering system has a base of 10 (MOD-10) and uses the digits from 0 through 9 to represent a decimal number value.

Binary – The binary numbering system has a base of 2 (MOD-2) and uses only two digits a “0” and a “1” to represent a binary number value.

Octal – The octal numbering system has a base of 8 (MOD-8) and uses 8 digits between 0 and 7 to represent an octal number value.

Hexadecimal – The Hexadecimal numbering system has a base of 16 (MOD-16) and uses a total of 16 numeric and alphabetic characters to represent a number value. Hexadecimal numbers consist of digits 0 through 9 and letters A to F. Long binary numbers are difficult to read or write and are generally converted into a different system which is user friendly.

The two most common derivatives based on binary numbers are the Octal and the Hexadecimal numbering systems, with both of these limited in length to a byte (8-bits) or a word (16-bits).

Octal numbers can be represented by groups of 3-bits and hexadecimal numbers by groups of 4-bits together, with this grouping of the bits being used in electronic or computer systems in displays or printouts.

The Comparisons between the various Decimal, Binary, Hexadecimal and Octal numbers are given in the following table.

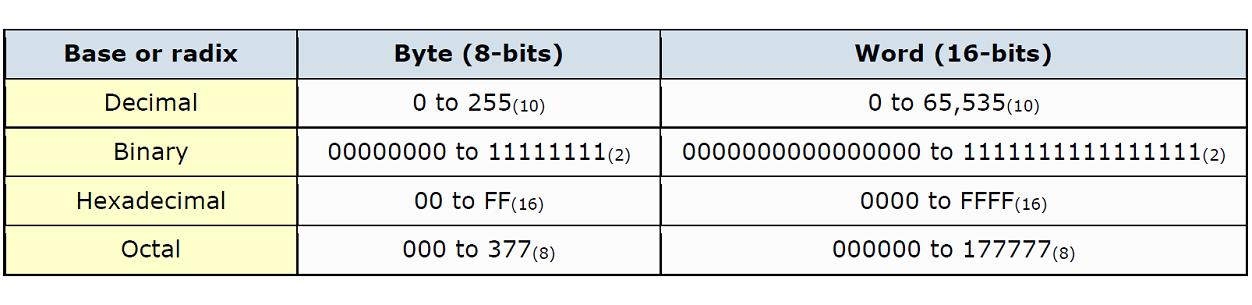
We can see from the table above that the Hexadecimal numbering system uses only four digits to express a single 16-bit word length, and as a result it is the most commonly used Base Numbering System for digital, micro-electronics and computer systems.

Numbering System

Decimal Number System

In the decimal number system, each integer number column has values of units, tens, hundreds, thousands, etc as we move along the number from right to left.

Mathematically these values are written as 100, 101, 102, 103 etc. Then each position to the left of the decimal point indicates an increased positive power of 10.

Likewise, for fractional numbers the weight of the number becomes more negative as we move from left to right, 10-1, 10-2, 10-3 etc.

The value of any decimal number will be equal to the sum of its digits multiplied by their respective weights.

For example: N = 616310 (Six Thousand One Hundred and Sixty Three) in a decimal format is equal to: 6000 + 100 + 60 + 3 = 6163 Or it can be written reflecting the weight of each digit as: (6×1000) + (1×100) + (6×10) + (3×1) = 6163

Or it can be written in polynomial form as:

(6×103) + (1×102) + (6×101) + (3×100) = 6163

Where in this decimal numbering system example, the left most digit is the most significant digit, or MSD, and the right most digit is the least significant digit or LSD.

In other words, the digit 6 is the MSD since its left most position carries the most weight, and the number 3 is the LSD as its right most position carries the least weight.

Binary Number System

The Binary Number System is the most fundamental number system in all digital and computer based systems and binary numbers follow the same set of rules as the decimal numbering system.

But unlike the decimal system which uses powers of ten, the binary numbering system works on powers of two giving a binary to decimal conversion from base-2 to base-10. Digital logic and computer systems use just two values or states to represent a condition, a logic level “1” or a logic level “0”, and each “0” and “1” is considered to be a single digit in a Base-of-2 or “binary number system”.
In electronics, binary numbers is the flow of information in the form of zeros and ones used by digital computers and systems.

Generally, a logic “1” represents a higher voltage, such as 5 volts, which is commonly referred to as a HIGH value, while a logic “0” represents a low voltage, such as 0 volts or ground, and is commonly referred to as a LOW value.

These two discrete voltage levels representing the digital values of “1’s” (one’s) and “0’s” (zero’s) are commonly called: BInary digiTS, and in digital and computational circuits and applications they are normally referred to as binary BITS.

Because there are only two valid Boolean values for representing either a logic “1” or a logic “0”, makes the system of using Binary Numbers ideal for use in digital or electronic circuits and systems.

Digital waveforms or signals consist of discrete or distinctive voltage levels that are changing back and forth between these two “HIGH” and “LOW” states. But what makes a signal or voltage “Digital” and how can we represent these “HIGH” and “LOW” voltage levels. Electronic circuits and systems can be divided into two main categories.

Analog Circuits – Analogue or Linear circuits amplify or respond to continuously varying voltage levels that can alternate between a positive and negative value over a period of time.

Digital Circuits – Digital circuits produce or respond too two distinct positive or negative voltage levels representing either a logic level “1” or a logic level “0”. In the binary number system, a binary number such as 101100101 is expressed with a string of “1’s” and “0’s” with each digit along the string from right to left having a value twice that of the previous digit. As the decimal number is a weighted number, converting from decimal to binary (base 10 to base 2) will also produce a weighted binary number with the right-hand most bit being the Least Significant Bit or LSB, and the left-hand most bit being the Most Significant Bit or MSB, and we can represent this as:

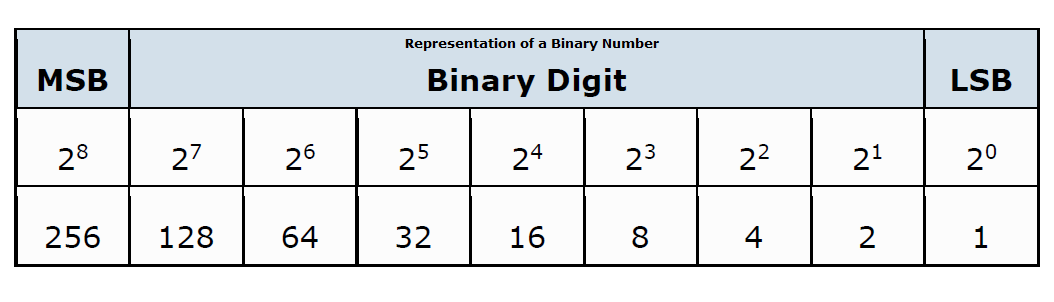
In the decimal number system, the weight of each digit to the left increases by a factor of 10. In the binary number system, the weight of each digit increases by a factor of 2 as shown.

Then the first digit has a weight of 1 (20), the second digit has a weight of 2 (21), the third a weight of 4 (22), the fourth a weight of 8 (23) and so on.

Conversion from Binary to Decimal

Conversion of binary to decimal (base-2 to base-10) numbers and back is an important concept to understand as the binary numbering system forms the basis for all computer and digital systems.

In a decimal system each digit has a value ten times greater than its previous number and this decimal numbering system uses a set of symbols, b, together with a base, q, to determine the weight of each digit within a number.

Any numbering system can be summarized by the following relationship:

N = bi qi where: N is a real positive number b is the digit q is the base value and integer (i) can be positive, negative or zero N = bn qn… b3 q3 + b2 q2 + b1 q1 + b0 q0 + b-1 q-1 + b-2 q-2… etc.

We can convert binary to decimal by finding the decimal equivalent of the binary array of digits 1011001012 and expanding the binary digits into a series with a base of 2 giving an equivalent of 35710 in decimal or denary.

For example, converting a Binary to Decimal number would be:

Decimal Digit Value 256 128 64 32 16 8 4 2 1

Binary Digit Value 1 0 1 1 0 0 1 0 1 By adding together ALL the decimal number values from right to left at the positions that are represented by a “1” gives us:

(256)+(64)+(32)+(4)+(1) = 357 base 10 or three hundred and fifty seven as a decimal number.

Conversion from Decimal to binary –  Repeated Division-by-2 Method

An easy method of converting decimal to binary number equivalents is to write down the decimal number and to continually divide-by-2 (two) to give a result and a remainder of either a “1” or a “0” until the final result equals zero.

So for example. Convert the decimal number 294 base 10 into its binary number equivalent.

Number 294 Dividing each decimal number by “2” as shown will give a result plus a remainder.

If the decimal number being divided is even then the result will be whole and the remainder will be equal to “0”.

If the decimal number is odd then the result will not divide completely and the remainder will be a “1”.

The binary result is obtained by placing all the remainders in order with the least significant bit (LSB) being at the top and the most significant bit (MSB) being at the bottom.

divide by 2

result 147 remainder 0 (LSB)

divide by 2

result 73 remainder 1

divide by 2

result 36 remainder 1

divide by 2

result 18 remainder 0

divide by 2

result 9 remainder 0

divide by 2

result 4 remainder 1

divide by 2

result 2 remainder 0

divide by 2

result 1 remainder 0

divide by 2

result 0 remainder 1 (MSB)

This divide-by-2 decimal to binary conversion technique gives the decimal number 294 base 10 an equivalent of 1001001102 in binary, reading from right to left.

This divide-by-2 method will also work for conversion to other number bases.

The main characteristics of a Binary Number System is that each “binary digit” or “bit” has a value of either “1” or “0” with each bit having a weight or value double that of its previous bit starting from the lowest or least significant bit (LSB) and this is called the “sum-of-weights” method.

Hence we can convert a decimal number into a binary number either by using the sum-of-weights method or by using the repeated division-by-2 method, and convert binary to decimal by finding its sum-of-weights.

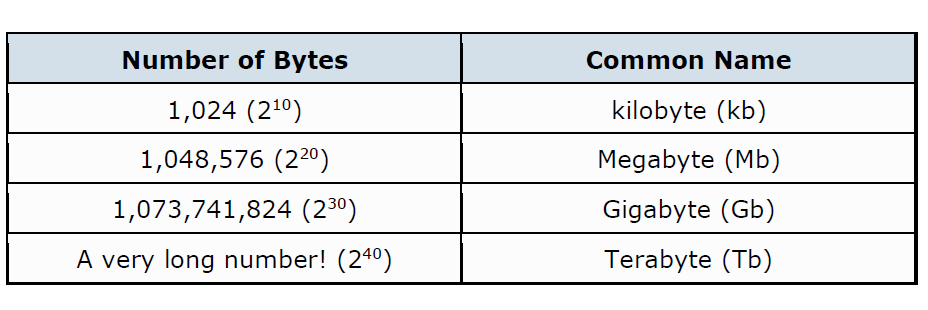
Binary Number Names & Prefixes

The binary numbers can be added together and subtracted just like decimal numbers with the result being combined into one of several size ranges depending upon the number of bits being used.

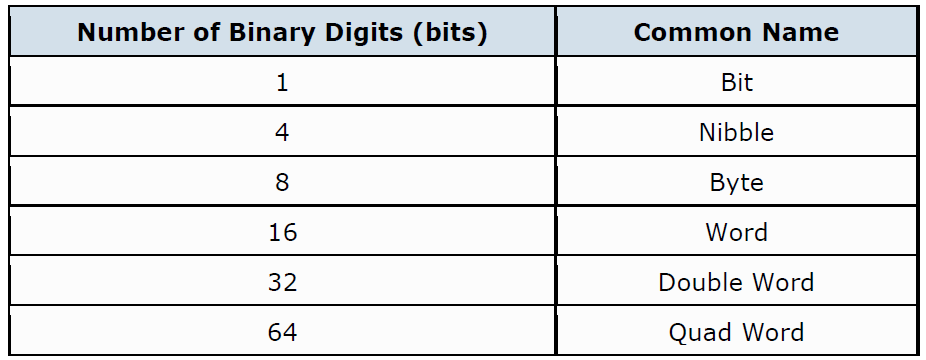
Binary numbers come in three basic forms – a bit, a byte and a word, where a bit is a single binary digit, a byte is eight binary digits, and a word is 16 binary digits.

The classification of individual bits into larger groups is generally referred to by the following more common names.

Also, when converting from Binary to Decimal or even from Decimal to Binary, we need to be careful that we do not mix up the two sets of numbers.

For example, if we write the digits 10 on the page it could mean the number “ten” if we assume it to be a decimal number, or it could equally be a “1” and a “0” together in binary, which is equal to the number two in the weighted decimal format from above.

One way to overcome this problem when converting binary to decimal numbers and to identify whether the digits or numbers being used are decimal or binary is to write a small number called a “subscript” after the last digit to show the base of the number system being used.

For example, if we were using a binary number string we would add the subscript “2” to denote a base-2 number so the number would be written as 102.

Likewise, if it was a standard decimal number we would add the subscript “10” to denote a base-10 number (written as 1010) 3.

Today, as micro-controller or microprocessor systems become increasingly larger, the individual binary digits (bits) are now grouped together into 8’s to form a single BYTE with most computer hardware such as hard drives and memory modules commonly indicate their size in Mb or Gb.

Binary to Decimal Summary

A “BIT” is the abbreviated term derived from BInary digiT

A Binary system has only two states, Logic “0” and Logic “1” giving a base of 2

A Decimal system uses 10 different digits, 0 to 9 giving it a base of 10

A Binary number is a weighted number who’s weighted value increases from right to left

The weight of a binary digit doubles from right to left

A decimal number can be converted to a binary number by using the sum-of-weights method or the repeated division-by-2 method

When we convert numbers from binary to decimal, or decimal to binary, subscripts are used to avoid errors.

Converting binary to decimal (base-2 to base-10) or decimal to Binary Numbers (base10 to base-2) can be done in a number of different ways as shown above.

When converting decimal numbers to binary numbers it is important to remember which the least significant bit (LSB) is, and which the most significant bit (MSB) is.