How to Convert Decimal Number to Binary Numbers

Conversion from decimal number to binary number system is also essential to represent real-world quantities in terms of Binary values.

The Sum-of-weights and repeated division by 2 methods are used to convert a decimal to Binary number.

Sum of Weights Method 

The  Sum-of-weights  method  used  to  convert  Binary  numbers  into  their  Decimal equivalent is based on adding binary weights of the binary number bits. Converting back from the decimal number to the original Binary number requires finding the highest weight included in the sum representing the decimal equivalent.

A Binary 1 is marked to represent the bit which contributed its weight in the Sum representing the decimal equivalent. The weight is subtracted from the sum decimal equivalent. The next highest weight included in the sum term is found.

A binary 1 is marked to represent the bit which contributed its weight in the sum term and the weight is subtracted from the sum term. This process is repeated until the sum term becomes equal to zero. The binary 1s and 0s represent the binary bits that contributed their weight and bits that did not contribute any weight respectively.

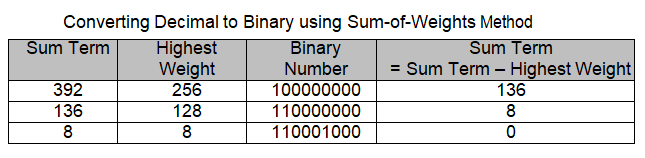
The process of determining Binary equivalent of a Decimal number 392 and 411 is illustrated in a tabular form.

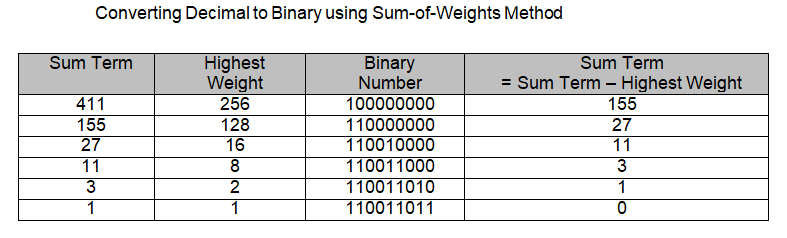
The  Sum  of  weights  method  requires  mental  arithmetic  and  is  a  quick  way  of converting small decimal numbers into binary. With practice large Decimal numbers can be converted into Binary equivalents.

Convert Decimal Number to Binary Numbers using Repeated Division

Repeated division-by-2 method allows decimal numbers of any magnitude to be converted into binary. In this method the decimal number to be converted into its Binary equivalent is repeatedly divided by 2.

The divisor is selected as 2 because the decimal number is being converted into binary a Base-2 Number system. Repeated division method can be used to convert decimal number into any Number system by repeated division by the Base- Number. For example, the decimal number can be converted into the Caveman Number system by repeatedly dividing by 5, the Base number of the Caveman Number System.

The Repeated Division method will be used in latter lectures to convert decimal into Hexadecimal and Octal Number Systems.

In the repeated-division method the decimal number to be converted is divided by the Base Number, in this particular case 2. A quotient value and a remainder value is generated, both values are noted done. The remainder value in all subsequent divisions would be either a 0 or a 1.

The quotient value obtained as a result of division by 2 is divided again by 2. The new quotient and remainder values are again noted down. In each step of the repeated division method the remainder values are noted down and the quotient values are repeatedly divided by the base number.

The process of repeated division stops when the quotient value becomes zero. The remainders that have been noted in consecutive steps are written out to indicate the Binary equivalent of the Original Decimal Number.

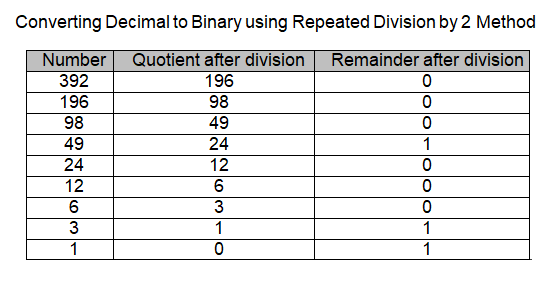
The  process  of  determining  the  Binary  equivalent  of  a  Decimal  number  392  is illustrated in a tabular form. Reading the numbers in the Remainder column from bottom to top 110001000 gives the binary equivalent of the decimal number 392.

Example of decimal to binary conversion

Digit mean human readable form, binary means computer readable form, so how I made this conversion above. Let’s see how make this conversion.

How the conversion is made

To make this conversion following formula is used,

n = is any number

We write obtained answer 1,2,4,8 in following manner.

Here in this above figure I mentioned, n = up to you wish.

8 4 2 1

But in here I considered n = 3 this simple form is used to convert decimal number into binary number.

Here I am going to explain how to make conversion of decimal into binary.

Ex :- convert 5 into binary form,

In here we can simply say that ,

decimal number 8 is stored binary number 0,

decimal number 4 is stored binary number 1,

decimal number 2 is stored binary number 0,

decimal number 1 is stored binary number 1,

Simple rules :-

• decimal number which stored zero is not considered,mean simply consider that number is delete.
• decimal number which stored one , that number is considered,mean simply consider that number is not deleted,it still live.

In the rule I said that the decimal which stores zero is not considered, because if we multiply any number with zero we get answer is zero.

In second rule I said that decimal number which stored one , that number is considered, because if we multiply any number with one we get answer is that of the same number.

By applying rule,

We get,

Now add remaining two decimal numbers,

= 4 + 1

= 5

What we get answer is five,

So binary of 5 is 0101 , understand

From this we can understand how to convert given number into binary.