Below is given the easiest Binary to decimal conversion method that you can do yourself even if you dont know the basic principle of mathematical conversion. In another artcile we have already described the manual conversion of binary to decimal numbers.
If you are willing to use computer for mathematical conversions then the best option is to use Excel sheets and applying the functions of binary t o decimal conversion. You can also use your smartphone if you have the Excel access on your device. Simply open the Excel and use below formula for Bin 2 Dec conversion.
Excel is also useful for finding binary to hexa and octal numbers by just changing the formula or function i.e. bin2hex & bin2oct.
BIN2DEC function
Syntax
BIN2DEC(number)
The BIN2DEC function syntax has the following arguments:
Number Required. The binary number you want to convert. Number cannot contain more than 10 characters (10 bits). The most significant bit of number is the sign bit. The remaining 9 bits are magnitude bits. Negative numbers are represented using two’s-complement notation.
If number is not a valid binary number, or if number contains more than 10 characters (10 bits), BIN2DEC returns the #NUM! error value.
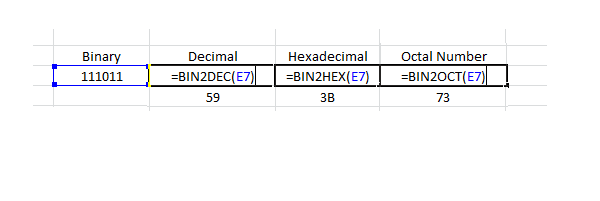
In below example screen shot E7 is the cell number where we have put the binary number 111011, we can directly insert the binary number inside the function argument i.e. in place of E7 in below screen image. This is also mentioned in below another example of binary to decimal conversion.
Example
Copy the example data in the following table, and paste it in cell A1 of a new Excel worksheet to get binary to decimal number. For formulas to show results, select them, press F2, and then press Enter. If you need to, you can adjust the column widths to see all the data.
| Formula | Description | Result |
| =BIN2DEC(1100100) | Converts binary 1100100 to decimal | 100 |
| =BIN2DEC(1111111111) | Converts binary 1111111111 to decimal | -1 |
binary to decimal conversion manual method
Step 1: Find out the total number of digits in the binary number for example it is having n digits.
Step 2: Subtract 1 from total number of digits this will be the power of the 2 for example if we have binary number 111010111 it is having 9 digits therefore by subtracting 1 we get number 8.
Step 3: Now start multiplying each binary digit with powers of 2 from 8 to zero and keep adding them as below:
1×28 = 256
1×27 = 128
1×26 = 64
0x25 = 0
1×24 = 16
0x23 = 0
1×22 = 4
1×21 = 2
1×20 = 1
Step 4: Now add all these values to get the decimal number: 471
Example No 2
Find the decimal value of 1110012:
| binary number: | 1 | 1 | 1 | 0 | 0 | 1 |
|---|---|---|---|---|---|---|
| power of 2: | 25 | 24 | 23 | 22 | 21 | 20 |
1110012 = 1⋅25+1⋅24+1⋅23+0⋅22+0⋅21+1⋅20 = 5710
Binary to decimal conversion table
| Binary Number |
Decimal Number |
Hex Number |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 10 | 2 | 2 |
| 11 | 3 | 3 |
| 100 | 4 | 4 |
| 101 | 5 | 5 |
| 110 | 6 | 6 |
| 111 | 7 | 7 |
| 1000 | 8 | 8 |
| 1001 | 9 | 9 |
| 1010 | 10 | A |
| 1011 | 11 | B |
| 1100 | 12 | C |
| 1101 | 13 | D |
| 1110 | 14 | E |
| 1111 | 15 | F |
| 10000 | 16 | 10 |
| 10001 | 17 | 11 |
| 10010 | 18 | 12 |
| 10011 | 19 | 13 |
| 10100 | 20 | 14 |
| 10101 | 21 | 15 |
| 10110 | 22 | 16 |
| 10111 | 23 | 17 |
| 11000 | 24 | 18 |
| 11001 | 25 | 19 |
| 11010 | 26 | 1A |
| 11011 | 27 | 1B |
| 11100 | 28 | 1C |
| 11101 | 29 | 1D |
| 11110 | 30 | 1E |
| 11111 | 31 | 1F |
| 100000 | 32 | 20 |
| 1000000 | 64 | 40 |
| 10000000 | 128 | 80 |
| 100000000 | 256 | 100 |
