1 Mega-ohm (MQ) = 10 6 Q
1 kilo-ohm (kQ) =10 3 Q
1 milli -ohm (mQ) = 10 -3 Q
1 micro-ohm (µ2) = 10 -6 Q
Laws of resistance
The resistance of a conductor, such as a wire, of uniform cross- section depends on the following factors:
(i) Length (l) : varies directly as its length,
(ii) Cross-section (A) : varies inversely as the cross-section, A, of the conductor
(iii) Nature of the material (p)
(iv) Temperature of the conductor: It almost varies directly with the temperature
R = p l / A
where p is known as specific resistance or resistivity.
Specific resistance or resistivity of a material may be defined as “The resistance between the opposite faces of a meter cube of that material”. The unit of resistivity is ohm-metre (Q-m).
Conductance (G) :
Conductance (G) is the reciprocal of resistance (G = 1 / R = A / pl)
Conductivity (σ):
The reciprocal of specific resistance ( σ = 1 /p) of a material is called its conductivity.
The unit of conductivity ( σ = G l / A) is mho/metre.
Temperature co-efficient of resistance :
Temperature co-efficient of resistance at 0°c may be defined as follows :
“The change in resistance per ohm for change in temperature of 1°C from 0°C”.
Over large temperature ranges the simple formula
Rt = Ro ( 1 + ∝ t)
does not completely fit, but a formula of the type
Rt = Ro ( 1 + ∝ t + β t2)
(where β is a smaller co-efficient) applies.
Pt = Po ( 1 + ∝o . t )
where p1 and p0 are the resistivities at to and 0°C respectively.
The Effect of temperature on resistance
The following points are worth noting :
The resistance of metal conductors ‘increases’ (a, i.e., temperature co-efficient of resistance being positive) with rise of temperature; the rate of increase is very considerable for most pure metals, being as much as about 1/1.50 of the total resistance for each centigrade rise in the case of iron; the effect is smaller in case of alloys, and very small indeed for materials such as manganin and constantan which are therefore very suitable for making standard resistances.
The resistance of semiconductors such as carbon, and all electrolytes ‘decreases’ as the temperature rises (a being negative).
Ohm’s Law & Resistance
– Ohm’s law can be stated as follows :
“For a fixed metal conductor, the temperature and other conditions remaining constant the current (1) through it is proportional to the potential difference (V) between its ends”.
In other words, V / I = constant or V /I = R
where R is the resistance of the conductor between the two points considering:
The linear relationship (I = V) does not apply to all non-metallic conductors. For example, for silicone carbide, the relationship is given by :
V = Kr where K and x are constants and x is less than unity.
The following relations hold good :
- p= VI = I2 R = V2 / R
- I = P/V = √P/R
- R = P / I2 = V2 / P
- V = P/I = √PR
Also the sum of all the voltage drops (V1 + V2 + V3) is equal to the applied voltage (V).
i.e. V= V1 + V2 + V3 [using Ohm’s law : V = IR]
IR = IR1 + IR2 + IR3
i.e. R = R1 + R2 + R3
where R is the equivalent resistance of series combination.
Resistances in parallel
Refer Figure below. In this case voltage across each resistance will be same but current will be different depending upon the value of the individual resistance.
I = I1 + I2 + I3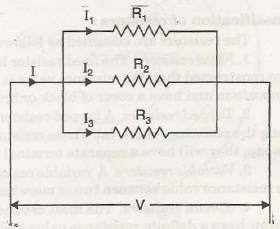
V / R = V / R1 + V / R2 + V / R3
1 / R = 1 / R1 + 1 / R2 + 1 / R3
where R is the equivalent resistance of the parallel combination.
R = R1 R2 R3 / R1 R2 + R2 R3 + R3 R1
G = G1 + G2 + G3
Resistivities and Temperature Co-efficients

Superconductivity
Equation Rt = R[l + a(t – 20)] holds good for temperature below 20°C. But at very low temperature, some metals acquire zero electrical resistance and zero magnetic induction; the property known as superconductivity.
Superconducting elements include Zinc, cadmium, mercury, lead. Typical superconducting compounds and alloys are PbAu, PbTh, SnSb, CuS, NbN, NbB, ZrC. The superconductivity will disappear if the temperature of the material is raised above its critical temperature, or, a sufficiently strong magnetic field or current density is employed.
Discover more from Electrical Engineering 123
Subscribe to get the latest posts sent to your email.

