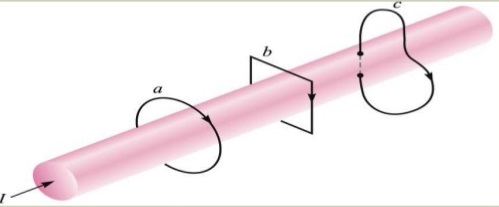
Ampere’s circuital law states that the line integral of magnetic field intensity about any closed path is exactly equal to the direct current enclosed by that path. In the figure below, the integral of H about closed paths a and b gives the total current I, while the integral over path c gives only that portion of the current that lies within c.
James Clerk Maxwell had derived that ampere’s circuital law. It alternatively says, the integral of magnetic field intensity (H) along an imaginary closed path is equal to the current enclosed by the path. 
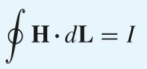
In another way we can define Ampere’s Circuital Law as the relationship between the current and the magnetic field created by the current. This law says, the integral of magnetic field density (B) along an imaginary closed path is equal to the product of current enclosed by the path and permeability of the medium. 
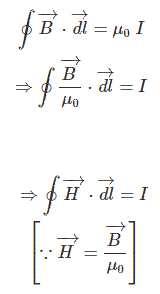
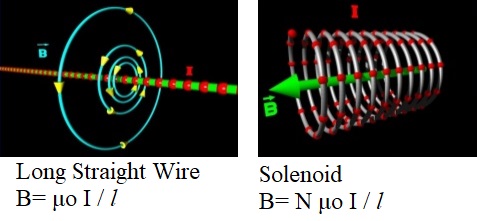
Ampere’s Circuital Law applied to long straight wires
The value of the magnetic field near a long straight wire is directly to proportional to the current in the wire. The magnetic field is inversely proportional to the distance from the wire.
Therefore we get two equations i.e. B α I and B α 1/r
In order to make this an equation multiply to the proportionality constant.
B= kI/r & K = μo/2π where μo = 4π x 10-7 T . m/A
Now we shall get B= μoI/2πr and the most general form is B= μoI / l
Note that it really isn’t the distance from the wire, but the circumference of the circle that the magnetic field circumvents.
Ampere’s Circuital Law and Solenoids
A solenoid can be considered to be a set of circular loops placed side by side that carry the same current. It produces a uniform magnetic field inside it. We can place this into Ampere’s Law equation as number of loops per unit length.
B= N μoI / l
