Windmill is very famous source of generating energy/electricity in the areas where basic infrastructure is not present i.e. in remote areas, farms and fields etc. Different types of windmills are available to install which we have covered in more detail in our article about windmill construction and operation.
Wind energy generation has evolved over the years to emerge as key renewable energy generation method. All countries in the world receive wind strong enough to generate some wind energy. It is expected that demand for wind turbines will increase, mainly fueled by China, Germany and the US.
As per Ken Research Report, significant contribution is expected to come from India and South Africa. Larger size turbines (greater than 2 MW) will be in great demand and is expected that cost of installation per MW will fall further. Many of the offshore wind projects will use turbines of a size greater than 5 MW.
Share of offshore wind turbine is expected to increase by the end of 2021. It is expected that unit cost of wind turbine per MW will register a continuous decline in future as technology improves and better efficiency and height is achieved. Service market is expected to gain substantial boost from aging turbines in the European and the US market.
How a Windmill Works
Most common type of windmill is horizontal axis which has some advantages and disadvantages as well. Below is a diagram that shows how a windmill works to generate wind power. Inflow of the air activates blades of a windmill which ultimately spins the rotor. Hence main shaft and gearbox also start spinning. This results generator spinning resulting the generation of electricity.
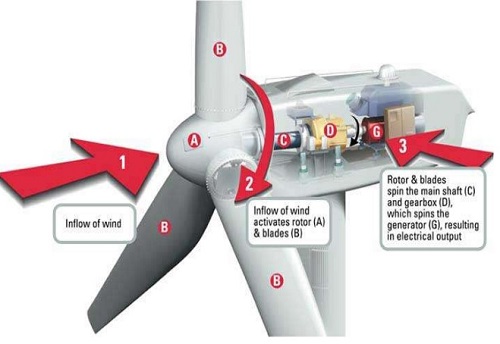
Theory of Wind Turbine / Windmill
For determining power extracted from wind by wind turbine we have to assume a air duct as shown in the figure. It is also assumed that the velocity of wind at the inlet of the duct is V1 and velocity of air at the outlet of the duct is V2. Say, mass m of the air is passed through this imaginary duct per second.
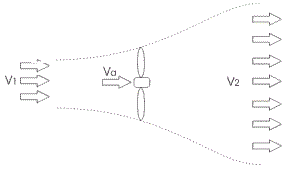
Now due to this mass the kinetic energy of wind at the inlet of the duct is,
![]()
Similarly, due this mass the kinetic energy of wind at the outlet of the duct is,
![]()
Hence, kinetic energy of wind changed, during flow of this quantity of air from inlet to outlet of the imaginary duct is,

As we already said that, mass m of the air is passed through this imaginary duct in one second, hence the power extracted from the wind is same as the kinetic energy changed during flow of mass m of the air from inlet to outlet of the duct. Since, power is defined as change of energy per second. Hence, this extracted power can be written as,
![]()
As mass m of the air passes in one second, the quantity m is referred as mass flow rate of the wind. If we think of that carefully, we can easily understand that mass flow rate will be same at inlet, at outlet and as well as at every cross – section of the air duct. This is because, whatever quantity of air is entering the duct, the same is coming out from the outlet.
If Va, A and ρ are the velocity of the air, cross – sectional area of the duct and density of air at the turbine blades respectively, then mass flow rate of the wind can be represented as,
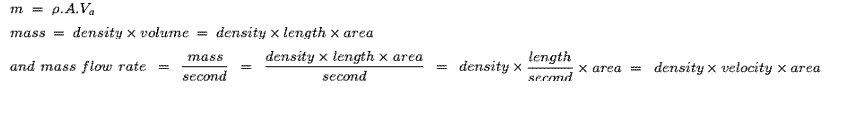
Now, replacing m by ρVaA in equation (1), we get,
![]()
Now, as the turbine is assumed to be placed at the middle of the duct, the wind velocity at windmill or turbine blades can be considered as average velocity of inlet and outlet velocities.

To obtain maximum power from wind, we have to differentiate equation (3) in respect of V2 and equate it to zero. That is,

From, the above equation it is found the theoretically maximum power extracted from the wind is in the fraction of 0.5925 of it’s total kinetic power. This fraction is known as Betz Coefficient. This calculated power is according to theory of wind turbine but actual mechanical power received by the generator is lesser than that and it is due to losses for friction rotor bearing and inefficiencies of aerodynamic design of the turbine.
From equation (4) it is clear that the extracted power is
1) Directly proportional to air density ρ. As air density increases, the power of the turbine increases.
2) Directly proportional to swept area of the turbine blades. If the length of the blade is increased, the radius of the swept area increases accordingly so turbine power increases.
3) Turbine power also varies with velocity3 of the wind. That indicates it velocity of wind is doubled, the turbine power will increase to eight folds.
Discover more from Electrical Engineering 123
Subscribe to get the latest posts sent to your email.

